In probability theory, the normal (or Gaussian) distribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Wikipedia
Es decir Normal Distribution y Gaussian Distribution es lo mismo.
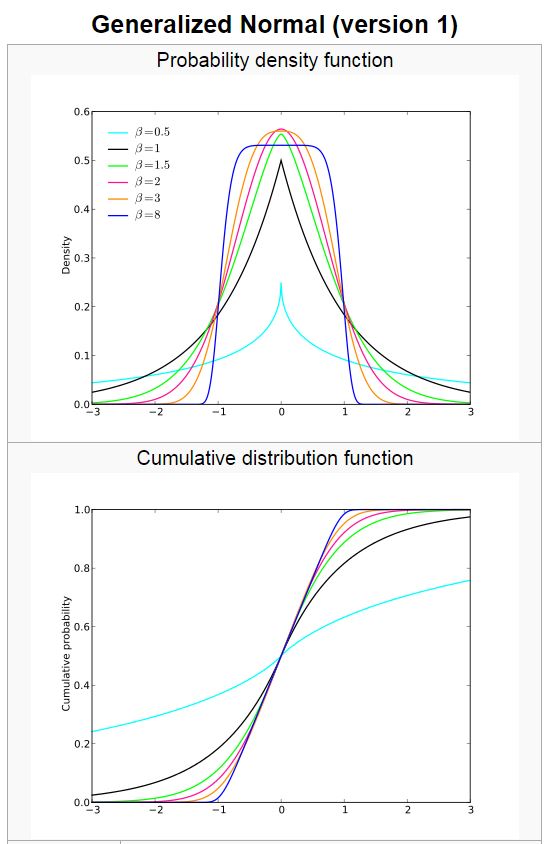
Generalized viene de que via un parámetro que se añade a la distribución normal, la distribución GGD puede adoptar distintas formas. Hay dos versiones, trataremos la versión 1 que es la que se utiliza para errores, imagenes, etc…
GGD: Known also as the exponential power distribution, or the generalized error distribution, this is a parametric family of symmetric distributions. It includes all normal and Laplace distributions, and as limiting cases it includes all continuous uniform distributions on bounded intervals of the real line. Wikipedia
La PDF (Probability Density Function) está definida con distintas formulas depende donde lo mires, pero depende de un parámetro para obtener su aspecto.
![Rendered by QuickLaTeX.com \[ GG(x,\alpha,\beta)=\frac{\beta}{2\alpha\Gamma (\frac{1}{\beta})} e^{-(\frac{\left | x-\mu \right |}{\alpha})^{\beta}} \]](https://momrach.es/wp-content/ql-cache/quicklatex.com-3ec74bb4ebc3150c425bb516524bf15b_l3.png)
donde ![]() es la función Gamma
es la función Gamma
Siguiendo la formula el parámetro ![]() hace que la distribución sea la Normal cuya media es
hace que la distribución sea la Normal cuya media es ![]() y su varianza es
y su varianza es ![]() .
.
Si ![]() la distribución será una Laplaciana.
la distribución será una Laplaciana.
Y si ![]() tenemos una distribución uniforme centrada en
tenemos una distribución uniforme centrada en ![]() y con amplitud entre
y con amplitud entre ![]()
La varianza de una GGD es 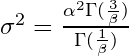
En el caso de ![]() (distribución normal) la varianza es
(distribución normal) la varianza es ![]() como hemos dicho porque las funciones
como hemos dicho porque las funciones ![]() y
y ![]() toman valores
toman valores ![]() y
y ![]() respectivamente. Estos valores particulares de Gamma se pueden ver en Valores Particulares de Gamma
respectivamente. Estos valores particulares de Gamma se pueden ver en Valores Particulares de Gamma
Por tanto, si conozco la varianza de una distribución de coeficientes por ejemplo, y sabiendo que la distribución de los coeficientes es una Laplaciana (![]() ), puedo despejar
), puedo despejar ![]() y con esto tendría la PDF de la distribución en concreto.
y con esto tendría la PDF de la distribución en concreto.