De entre las etapas de la codificación de imagen y vídeo, la cuantización es la única en la que se…
Continue ReadingCategoría: Quantization
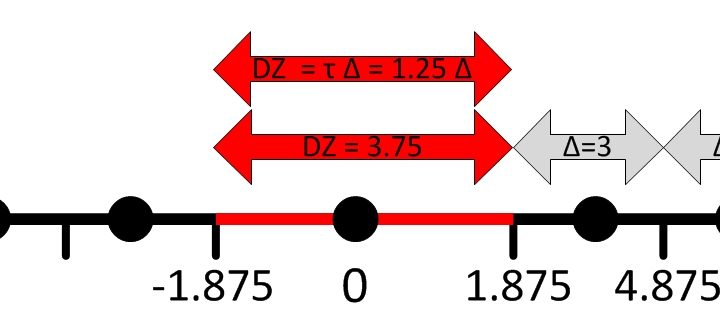
Calculo del tamaño del Dead Zone
El tamaño del dead zone en un UVDZQ (Uniform Variable Dead Zone Quantizer) depende de tres factores, , y .…
Continue ReadingSeguimiento 17 Mayo 2013
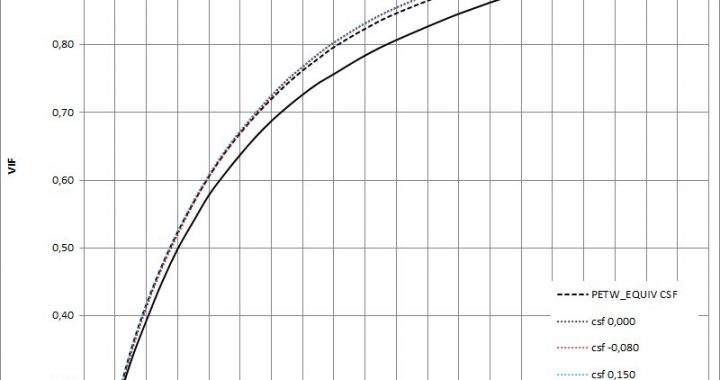
Corrección del cuantizador en PETW Tras ver las diferencias en las curvas R/D entre el PETW y el S_LTW y…
Continue ReadingQuantización ecualizada tras rate-control
Cuando esté realizado el rate-control uniforme tras la ponderación/cuantización perceptual se supone que tendremos una q que ajustará al rate…
Continue Reading