Quantizers formulation – Miguel Onofre Martínez Rach

Here is some formulation for some of the most widelly used quantizers in image and video compression standards. Not only the direct and inverse quantization step formulation is shwon but also the formulation to calculate the lower and upper bounds, the centroid and the reconstruction point of each decission interval based on parameter $n$ (the decission interval index)

In the next equations:

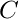$C$ is the transformed coefficient before quantization
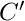$C'$ is the quantized coefficient after the direct quantization step
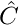$\hat{C}$ is the recovered value after the inverse quantization step
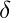$\delta$ is a constant used for defining the recovering location in each quantization interval. Allowed values are in the interval $\left [ 0..1 \right ]$
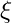$\xi$ is a contant used for defining the size of the deadzone. Allowed values are in the interval $\left ( -\infty ..1 \right ]$
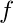$f$ is an offset or also known as rounding factor that sets the width of the deadzone.
$\Delta$ stands for the quantization step size or QStep
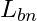$L_{bn}$ is the value of the lower bound of the decision bin or quantization step with index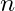 $n$
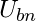$U_{bn}$ is the value of the upper bound of interval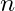 $n$
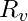$R_v$ is the value recovered for interval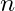 $n$
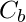$C_b$ is the value in the center of interval $n$ .

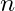USQ – Uniform Scalar Quantizer

This is the general uniform quantizer in its mid-tread form.

General Formulation:

$C'=sign(C)\left \lfloor \frac{\left | C \right |}{\Delta} + \frac{1}{2} \right \rfloor$

$\hat{C} = \Delta C'$

Quantization Intervals Formulation:

$n=0 \rightarrow \left\{\begin{matrix} L_{bn} = - \frac{\Delta}{2} \\ U_{bn} = \frac{\Delta}{2} \\ R_v = C_d = 0 \end{matrix}\right$

$n \neq 0 \rightarrow \left\{\begin{matrix} L_{bn} = \frac{\Delta}{2}(2n-1) \\ U_{bn} = \Delta (n+1) - \frac{\Delta}{2} \\ R_v = C_d = \Delta n \end{matrix}\right$

UDZQ – Uniform Dead Zone Quantizer

This is the formulation for a standard quantizer with deadzone twice the size of the Qstep.

General Formulation:

$C'=sign(C)\left \lfloor \frac{\left | C \right | }{\Delta} \right \rfloor$

$\hat{C} = sign(C')(\left | C' \right | + \delta ) \Delta$

Quantization Intervals Formulation:

$n=0 \rightarrow \left\{\begin{matrix} L_{bn} = -\Delta \\ U_{bn} = \Delta \\ R_v = C_d = 0 \end{matrix}\right$

$n > 0 \rightarrow \left\{\begin{matrix} L_{bn} = \Delta n \\ U_{bn} = \Delta(n+1) \\ R_v = \Delta (n + \delta) \\ C_d = \Delta n + \frac{\Delta}{2} \end{matrix}\right$

$n < 0 \rightarrow \left\{\begin{matrix} L_{bn} = \Delta (n-1) \\ U_{bn} = \Delta n \\ R_v = \Delta (n - \delta) \\ C_d = \Delta n - \frac{\Delta}{2} \end{matrix}\right$

UDZQ+O – Uniform Dead Zone Quantizer + Offset

General Formulation:

$C'= sign(C)\left \lfloor \frac{\left | C \right | + f }{\Delta} \right \rfloor$

$\hat{C} = C' \Delta$

Quantization Intervals Formulation:

$n=0 \rightarrow \left\{\begin{matrix} L_{bn} = -\Delta + f \\ U_{bn} = \Delta - f \\ R_v = C_d = 0 \end{matrix}\right$

$n > 0 \rightarrow \left\{\begin{matrix} L_{bn} = \Delta n -f \\ U_{bn} = \Delta (n+1)-f \\ R_v = \Delta n \\ C_d = \Delta (n + \frac{1}{2}) - f \end{matrix} \right$

$n < 0 \rightarrow \left\{\begin{matrix} L_{bn} = \Delta (n-1)+ f \\ U_{bn} = \Delta (n)+ f \\ R_v = \Delta n \\ C_d = \Delta (n - \frac{1}{2}) +f \end{matrix}\right$

UVDZQ – Uniform Variable Dead Zone Quantizer.

General Formulation:

$C'= \left\{\begin{matrix} sign(C)\lfloor \frac{\left | C \right | +\xi \Delta}{\Delta} \rfloor & if \left | C \right | \geq -\xi\Delta \\ 0 & if \left | C \right | < -\xi\Delta \end{matrix}\right$

$\hat{C} = \left\{\begin{matrix} sign(C')(\left | C' \right | - \xi + \delta ) \Delta & if C' \neq 0 \\ 0 & if C' =0 \end{matrix}\right.$

Quantization Intervals Formulation:

$n=0 \rightarrow \left\{\begin{matrix} L_{bn} = \Delta (\xi-1) \\ U_{bn} = \Delta (1-\xi) \\ R_v = C_d = 0 \end{matrix}\right$

$n > 0 \rightarrow \left\{\begin{matrix} L_{bn} = \Delta (n-\xi) \\ U_{bn} = \Delta (n+1-\xi) \\ R_v = \Delta (n-\xi+\Delta)-\delta \\ C_d = \Delta (n-\xi)+\frac{\Delta}{2} \end{matrix}\right$

$n < 0 \rightarrow \left\{\begin{matrix} L_{bn} = \Delta (n-1+\xi) \\ U_{bn} = \Delta (n+\xi) \\ R_v = \Delta (n+\xi-\Delta)+\delta \\ C_d = \Delta (n+\xi)-\frac{\Delta}{2} \end{matrix}\right$