Corrección del cuantizador en PETW
Tras ver las diferencias en las curvas R/D entre el PETW y el S_LTW y revisar la cuantización en ambos no entendía porqué las curvas del PETW eran peores que las del S_LTW cuando la formulación revisada de ambos (la teoría) indicaba que los datos cuantizados y decuantizados debían ser los mismos.
La única diferencia que podía hacer que las curvas fueran distintas es que añado dos simbolos más en la tabla de simbolos del aritmético para poder liberarnos del rplanes. Las diferencias eran demasiado grandes y me hacían sospechar.
Se ha vuelto a comprobar que el PETW con un (DZ) de 1.25Δ equivale exactamente al cuantizador del S_LTW que fija el DZ en 1.25Δ con la inclusión de K=1.5 en el código y mantiene todos los QSteps de tamaño fijo Δ. Las formulas en PETW y en la Tesis de Oliver (pag. 215)
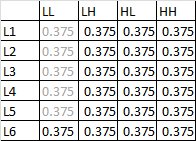
Por tanto PETW 1.25Δ = SLTW . La ξ para 1.25Δ = 0.375
ξ (según la formula) puede variar de -1 a 1.
Valores negativos de ξ aumentan el DZ de partida que es 2Δ.
Se ha incorporado una optimización que se hacía en el S_LTW en el PETW que corresponde a marcar como un bloque 2×2 como todo a ceros y su padre marcarlo como símbolo especial L.
Se han corregido distintos errores y se ha buscado que la secuencia de desplazamientos y cuantización sea la misma en los dos codificadores con lo que he tenido que introducir un un valor de ajuste φ=1 para eliminar un error que se produce por la secuencia <<, Q, >> . Este ajuste solo se aplica en el cuantizador, el decuantizador sigue la teoría estrictamente.
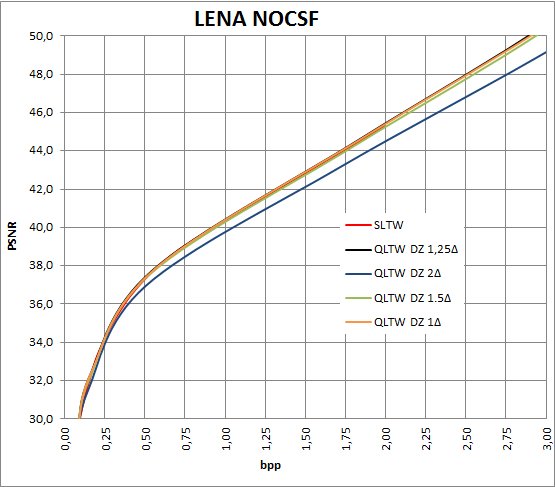
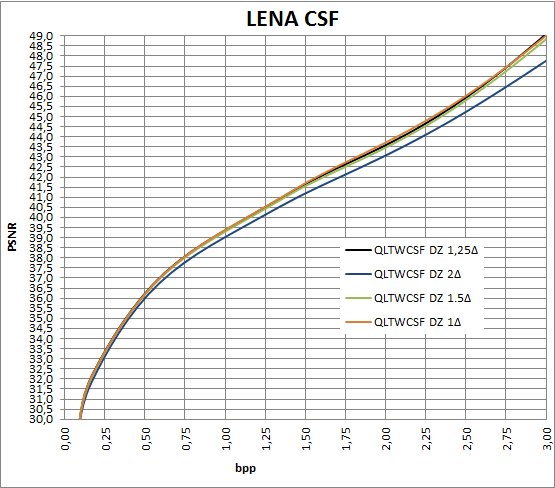
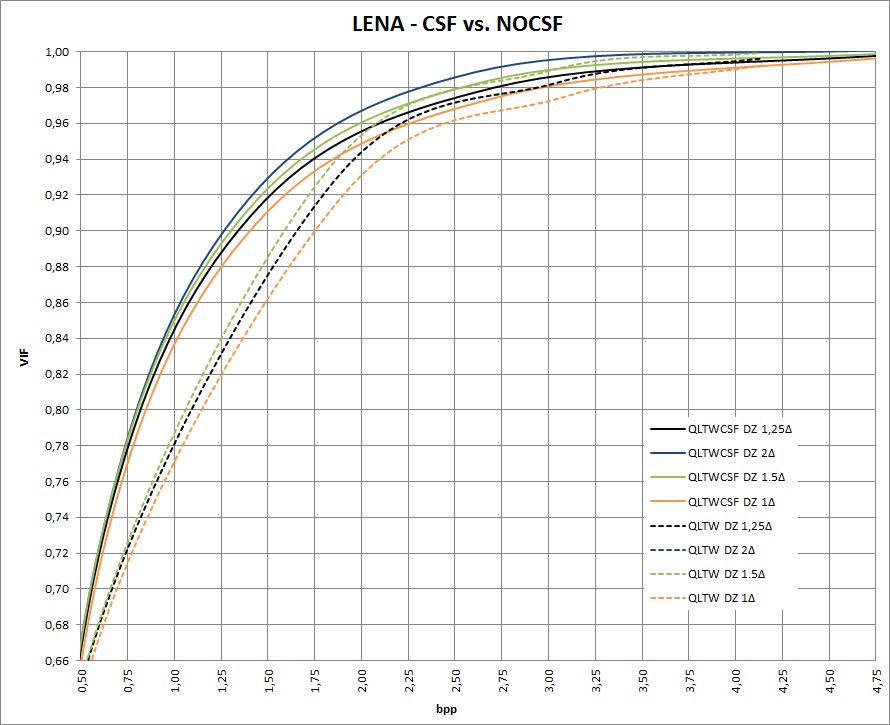
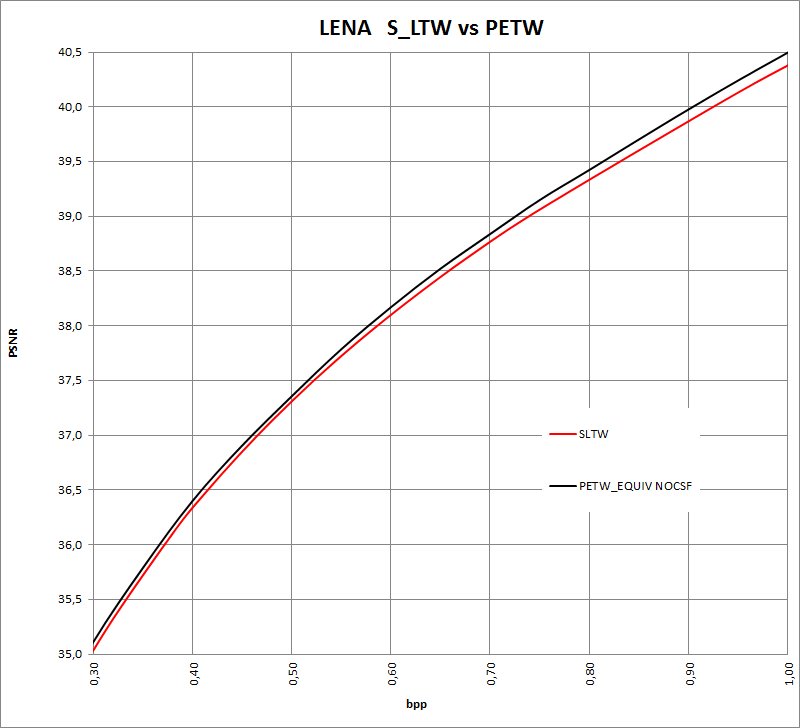
Las curvas en PSNR para Lena entre S_LTW y PETW quedan como sigue:
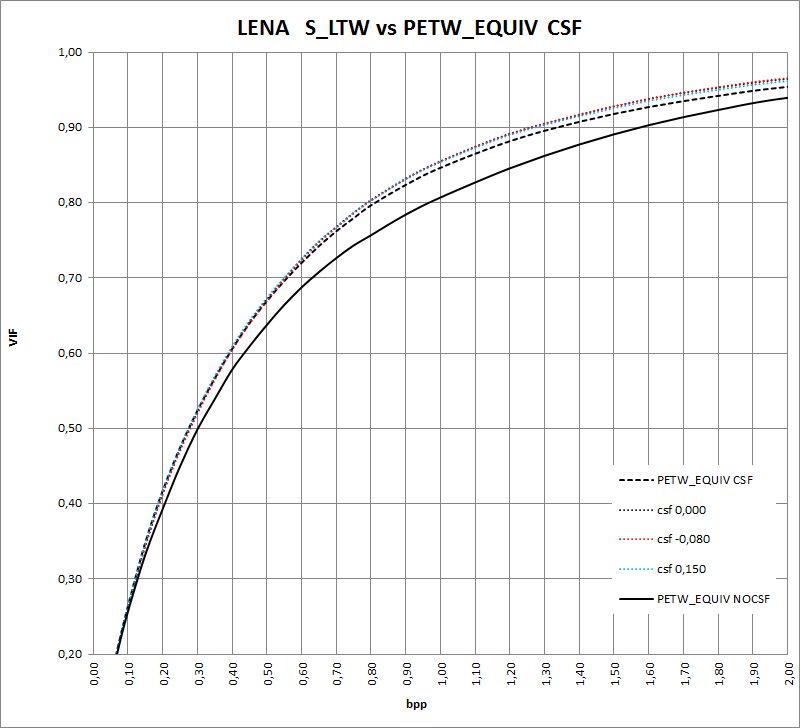
 Variaciones del DZ
Variaciones del DZ
Ahora que tenemos el codificador con el cuantizador correcto, podemos jugar con el DZ.
Variaciones del DZ afectan a la calidad, media en PSNR y de manera diferente, medida en VIF.
¿Que DZ es óptimo aplicado a todos los niveles?
Variando el DZ en el PETW mediante matrices globales de cuantización
Genero matrices globales para cada Xi en [-1 : 0.010: 1]
Para cada Xi genero con PETW, la curva (CSF y NoCSF) para las Qscsf=[0.5 2 5 15 80 250] Qsnocf=[0.5 1 2 6 20 40]
Realizo un Fitting para cada curva con una RAt21 (Matlab)
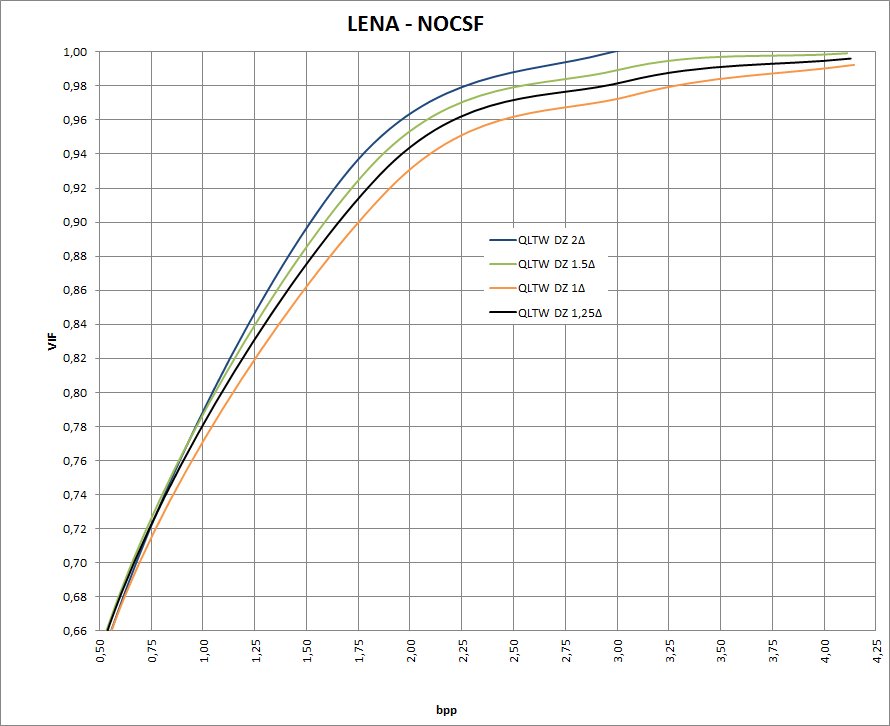
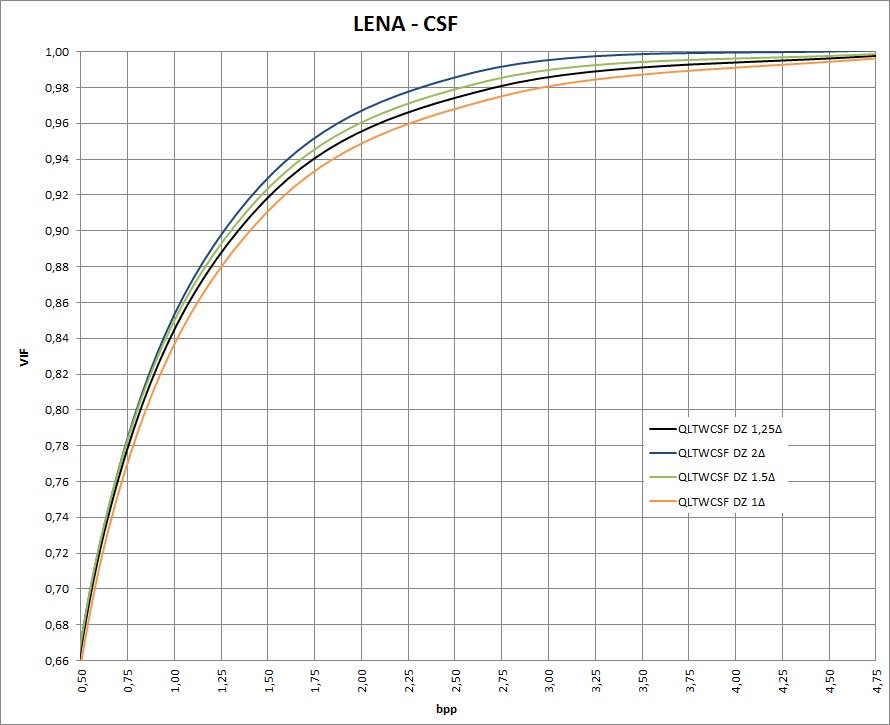
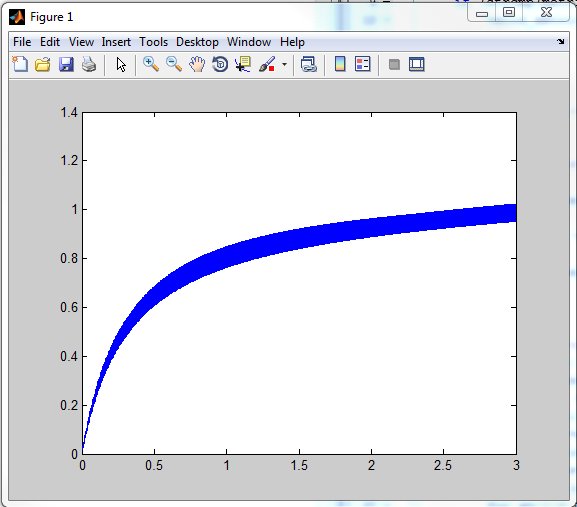
Esto genera las siguientes curvas (ploteadas en el mismo gráfico):
Como vemos la variación es grande, La peor de todas es para Xi=-1 .
¿Como calculo la mejor? -> La que mayor área tenga con el eje de abcisas.
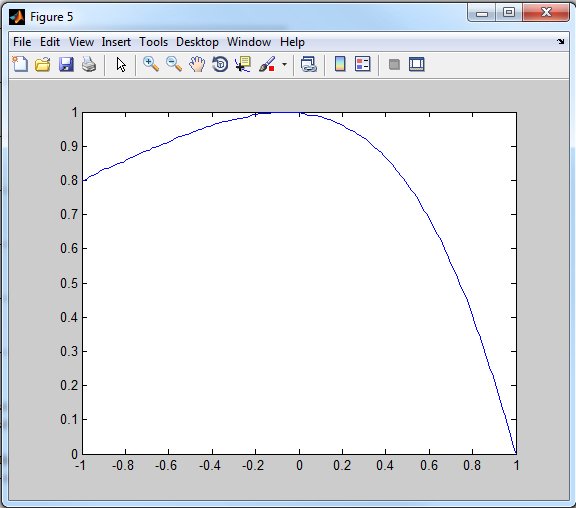
Con : [bestxi,rates,qvals]=GetBestVifRefCurve(‘lena’,’csf’,[0 3.0]) obtengo la siguiente gráfica muestra en en eje X los posibles Xi en la Y los valores del área normalizada en el rango [0 3.0] bpp
Vemos que para el rango [0 3.0] bpp el máximo está en Xi=-0.80 que corresponde con 2.18Δ
Los Optimos Globales varian con el rango.
Si nos centramos en el rango donde las diferencias son más visibles [0 0.4] bpp el BestXi varia a Xi=0.150 que corresponde con 1.70Δ
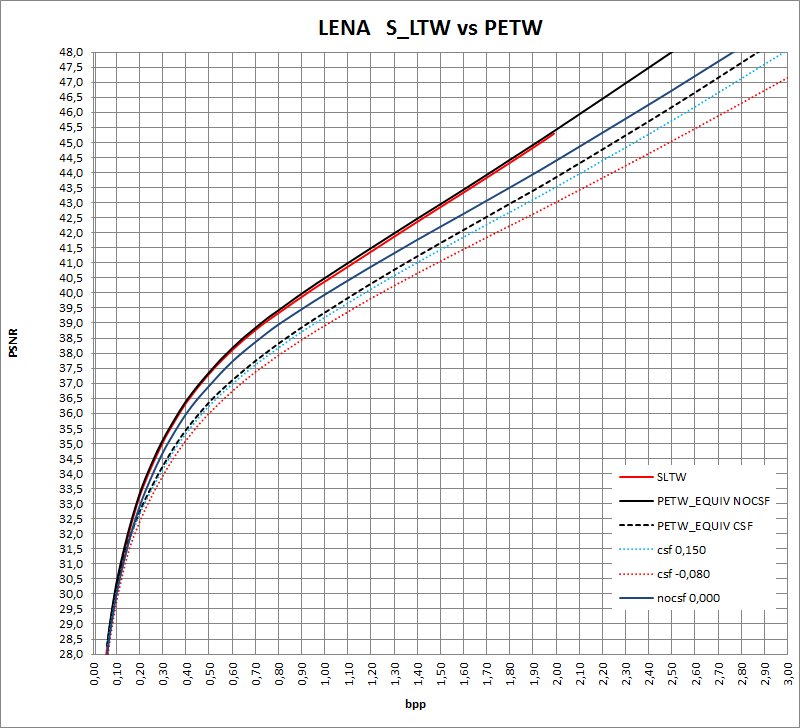
Estoy con : Buscando el mejor Xi para cada Nivel partiendo del mejor Xi que he seleccionado Xi=0.000 correspondiente a 2Δ a ver si cambia la curva….