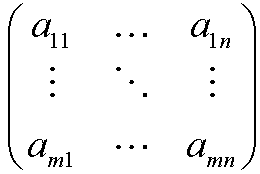De entre las etapas de la codificación de imagen y vídeo, la cuantización es la única en la que se…
Continue ReadingCategoría: Perceptual Quantization
GGD – Generalized Gausian Distribution
In probability theory, the normal (or Gaussian) distribution is a very common continuous probability distribution. Normal distributions are important in…
Continue ReadingCalculo de los CSF Weights
De cara a la escritura de la Tesis, en esta entrada voy a explicar cómo se calculan correctamente los CSF…
Continue ReadingSeguimiento 17 Mayo 2013
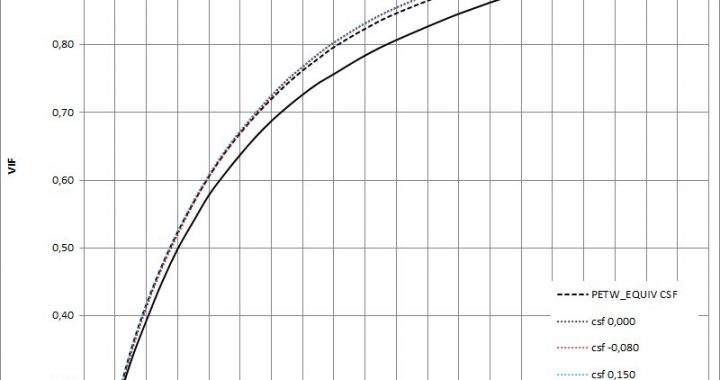
Corrección del cuantizador en PETW Tras ver las diferencias en las curvas R/D entre el PETW y el S_LTW y…
Continue ReadingAdaptive Coefficient Modification (ACM) (Filtro Nadenau)
La implementación correcta del filtrado para que no amplíe el tamaño de las subbandas se debe a la aplicación de…
Continue ReadingTest subbjetivo para determinar el delta-VIF mínimo
Parece evidente que la VIF es la métrica que mejor se ajusta (de las estudiadas) a la calidad subjetiva tras…
Continue ReadingQuantización ecualizada tras rate-control
Cuando esté realizado el rate-control uniforme tras la ponderación/cuantización perceptual se supone que tendremos una q que ajustará al rate…
Continue Reading