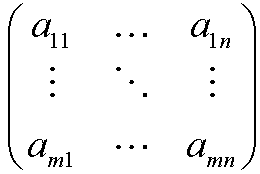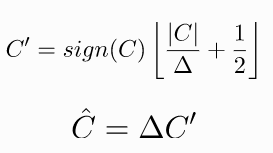De entre las etapas de la codificación de imagen y vídeo, la cuantización es la única en la que se…
Continue ReadingCategoría: Perceptual Coding
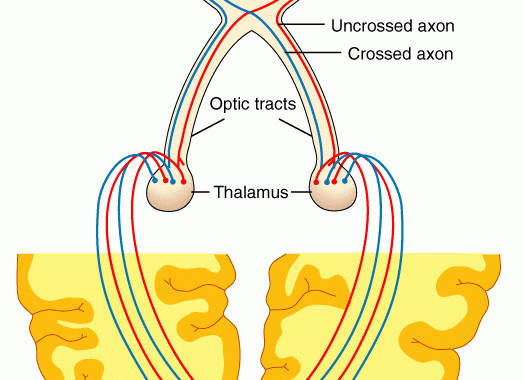
Características principales del HVS (Human Visual System) usadas en Codificación Perceptual de Imagen y Vídeo
Todo aquello que es perceptualmente redundante puede ser eliminado. Estas son las características fundamentales del sistema visual humano (HVS) que…
Continue ReadingQuantizers formulation
Here is some formulation for some of the most widelly used quantizers in image and video compression standards. Not only…
Continue ReadingCalculo de los CSF Weights
De cara a la escritura de la Tesis, en esta entrada voy a explicar cómo se calculan correctamente los CSF…
Continue ReadingReferencias CSF
CSFs Referencias a distintos modelos matemáticos de la Contrast Sensitivity Function.
Continue Reading